GSoC 2017 : A Wrapper for the FEniCS Finite Element Toolbox

Throughout this Google Summer of Code project I, along with my mentors, aimed to create a Wrapper for the FEniCS Finite Element Toolbox in the Julia Language. Our work done can be found at FEniCS.jl . This would allow users to perform FEM calculations directly in Julia, utilizing our PyCall.jl wrapping functionality. We currently have wrapped the main functionality, along with providing the necessary instructions to add further components when they are deemed necessary. Members of the Julia community not directly related to the project also contributed small fixes and suggestions throughout the project. The majority of the code produced has already been merged to the GitHub repository (which was created specifically for this project). One of the main improvements which would greatly increase its usage would be the further integration with the JuliaDiffEq package.

What is FEniCS?

FEniCS describes itself as a popular open-source (LGPLv3) computing platform for solving partial differential equations (PDEs). FEniCS enables users to quickly translate scientific models into efficient finite element code, i.e. it allows us to describe (some) complicated mathematical equations and solve them automatically using computer simulations.

But, how does it work?

The finite element method is a numerical method that solves partial differential equations by solving the weak form of a Galerkin approximation of the function into some sparse basis. This is done by discretizing the domain (breaking it up into small pieces, generally triangles called finite elements), representing the function via the values at the nodes of the triangles. This results in a system of equations which are an interpretation of the initial partial different equations in terms of the basis of these triangles. This is nearly impossible to do by hand, so computer software is required to aid in solving it. Our wrapper provides calls to the meshing functionality, the assembly of the stiffness matrices and the solution of the variational problems. It also provides access to various helper functions, that make usage easier. Some example meshes can be demonstrated below :

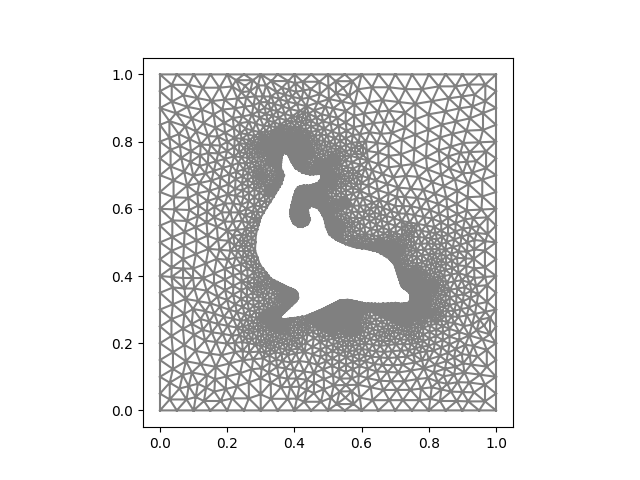
And, internally?

We currently provide macros to create Julia types from FEniCS classes to assist with function overloading. Apart from this we can wrap attributes and combining these two with PyCall.jl functionality we can wrap the necessary functions directly from FEniCS. We define methods for performing some linear algebra operations, and define operator functions +,-,* for various geometric objects and UFL forms. Our exported API remains approximately the same as the pythonic FEniCS with only very slight changes.

Demonstration

Below is a small demonstration of how a user would use our code to solve the Poisson equation with Dirichlet conditions. This directly mirrors one of the tutorials FEniCS provides

$-\bigtriangleup(u) = f$ in the unit square

$u = u_D$ on the boundary

$u_D$ $=$ $1 + x^2 + 2y^2$

$f = -6$

using FEniCS
mesh = UnitSquareMesh(8,8)
V = FunctionSpace(mesh,"P",1)
u_D = Expression("1+x[0]*x[0]+2*x[1]*x[1]", degree=2)
u = TrialFunction(V)
bc1 = DirichletBC(V,u_D, "on_boundary")
v = TestFunction(V)
f = Constant(-6.0)
a = dot(grad(u),grad(v))*dx
L = f*v*dx
U = FEniCS.Function(V)
lvsolve(a,L,U,bc1) #linear variational solver
errornorm(u_D, U, norm="L2")
get_array(L) #this returns an array for the stiffness matrix
get_array(U) #this returns an array for the solution values
vtkfile = File("poisson/solution.pvd")
vtkfile << U.pyobject #exports the solution to a vtkfile

Apart from just defining the problem, we can also access and save the arrays corresponding to various variational forms. These return an array type We can do this as follows :

a = dot(grad(u),grad(v))*dx #this sets up the variatonal form from the previous problem
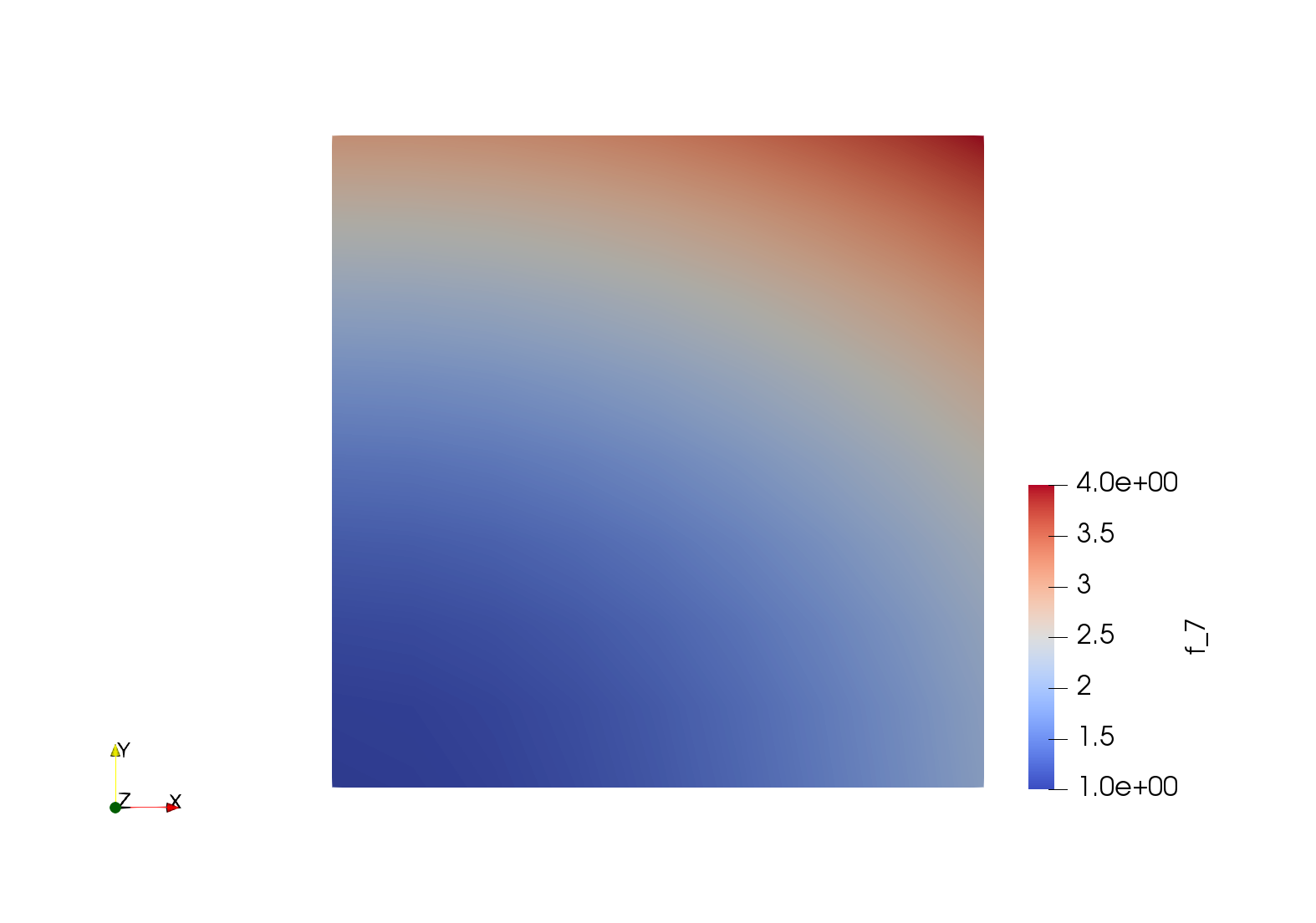
variational_matrix = get_array(a)

We can also plot the solution (this relies on FEniCS backend for plotting) :

FEniCS.Plot(mesh)
FEniCS.Plot(U)

Challenges

Due to the nature of this project, which relied on FEniCS, we faced various challenges throughout the summer. These included, but where not limited to build errors, where various parts of the package failed to compile, to unexpected errors in the usability of the code. Chris and Bart were very helpful, in both pointing these out, and in assisting in fixing them. In some parts the documentation was slightly patchy which also complicated parts of the project as some functions where ambiguous towards their intended use.

Further Improvements

I hope to be able to maintain and improve the package, using it where possibly throughout my further studies. Some identifiable improvements, in order of difficulty are :

• Fixing precompilation which would provide a large performance benefit. This error is well documented, and the fix is relatively simple. At the same time it would require the rewriting of a large segment of the codebase due to the way we currently access functions and attributes.

• Improving plotting. We currently rely on the FEniCS plotting backend to plot the necessary functions/meshes/objects. For more detailed visualization we can use Paraview, like in FEniCS. A direct Julia plotter would be nice, as we could provide further customization to our objects.

• Integration with JuliaDiffEq. We can currently specify and create the necessary objects for the solution of some FEM problems. We have also provided interfaces for accessing most of their attributes aswell as exporting the necessary arrays. Despite this, we currently have no automatic way of seamlessly accessing them via other packages. By providing this access, we would be able to greatly extend the packages capabilities.

• FEniCS itself is a collection of different components. The FFC(FEniCS Form Compiler) takes matrix assembly expressions and compiles these to C code and then further to machine code. A more optimal way of doing this, would be to replace the whole process with Julia code

On the Shoulders of Giants

Apart from coding, which was very enjoyable and provided a unique learning experience, undertaking this summer project introduced me to a wonderful community. In the brief time working alongside Julia, I had the opportunity to visit the Julia Computing offices in London. Right after, I was provided funding by Julia Computing and NumFOCUS to attend JuliaCon2017 and present a poster. Apart from the excellent talks, there I had the opportunity to share a flat with other GSoC students, and have lunch and drinks with pre-eminent members of the Julia Community. I truly believe this is one of the wonderful things about the open - source community. People devoting their time and effort, to help other people, and to propagate scientific discoveries open to everyone.

JuliaCon 2017 attendees

Acknowledgements

First and foremost I would like to thank my mentors Chris and Bart. Chris despite the significant timezone difference has always been there to answer my (very often) questions and provide suggestions. Bart has found lots of the initial errors and inconsistencies in the code, providing the necessary information to fix these errors. Julia Computing, who along with NumFOCUS, provided funding for me to attend JuliaCon 2017 and present a poster. Finally the Google Open Source program, who provided the necessary funding so I could undertake this project throughout the summer months and have a wonderful experience.