1091. Shortest Path in Binary Matrix

In an N by N square grid, each cell is either empty (0) or blocked (1).

A clear path from top-left to bottom-right has length k if and only if it is composed of cells C_1, C_2, ..., C_k such that:

• Adjacent cells C_i and C_{i+1} are connected 8-directionally (ie., they are different and share an edge or corner)
• C_1 is at location (0, 0) (ie. has value grid[0][0])
• C_k is at location (N-1, N-1) (ie. has value grid[N-1][N-1])
• If C_i is located at (r, c), then grid[r][c] is empty (ie. grid[r][c] == 0).

Return the length of the shortest such clear path from top-left to bottom- right. If such a path does not exist, return -1.

Example 1:

Input: [[0,1],[1,0]]
![](https://assets.leetcode.com/uploads/2019/08/04/example1_1.png)

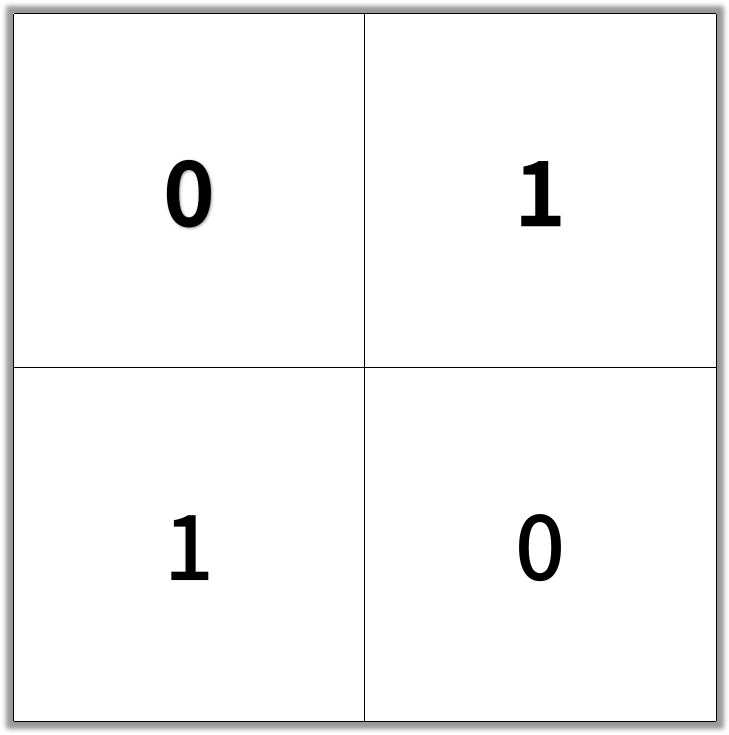
Output: 2
![](https://assets.leetcode.com/uploads/2019/08/04/example1_2.png)

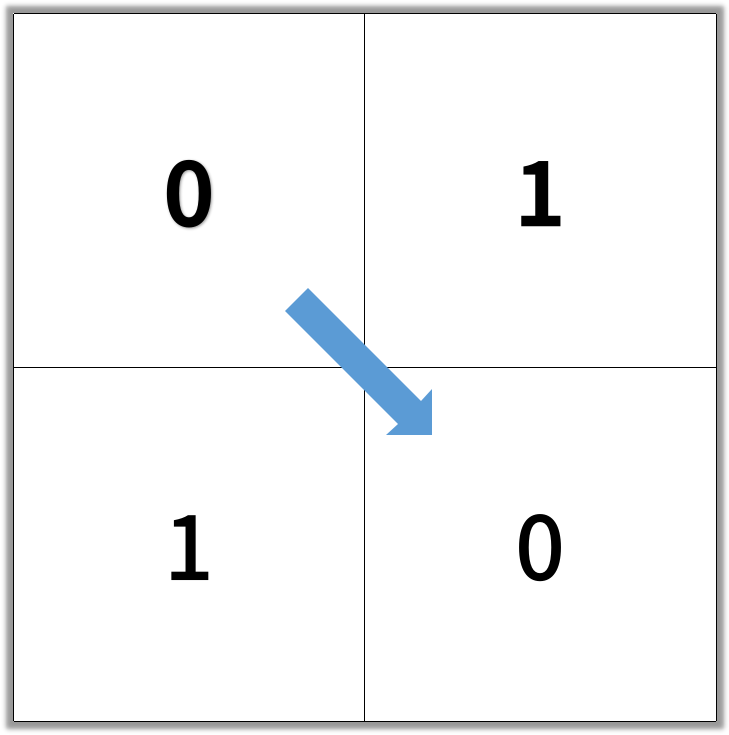Example 2:

Input: [[0,0,0],[1,1,0],[1,1,0]]
![](https://assets.leetcode.com/uploads/2019/08/04/example2_1.png)

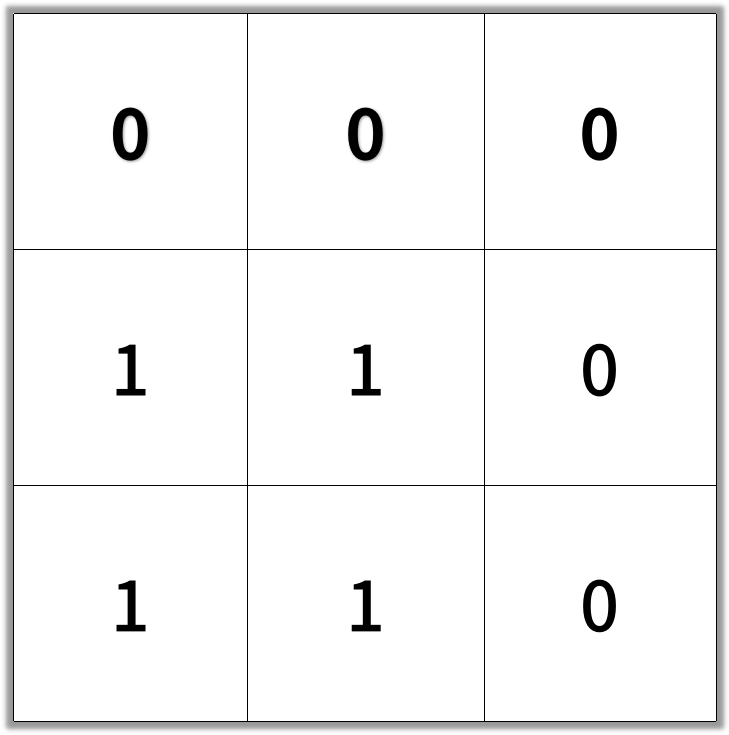
Output: 4
![](https://assets.leetcode.com/uploads/2019/08/04/example2_2.png)

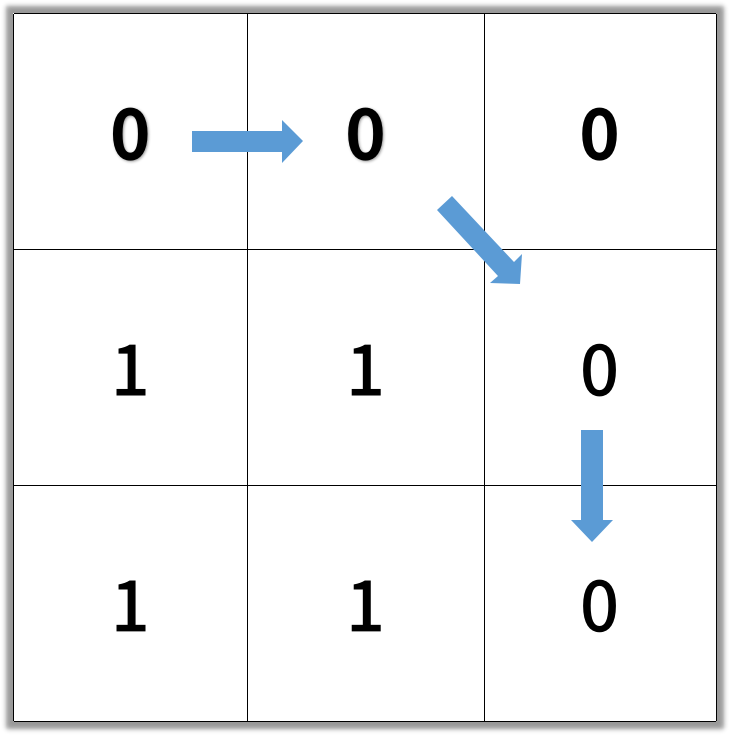Note:

1. 1 <= grid.length == grid[0].length <= 100
2. grid[r][c] is 0 or 1

# @lc code=start
using LeetCode

function shortest_path_binary_matrix(mat::Matrix{Int})
    visited = fill(false, size(mat))
    q = [CartesianIndex(1, 1)]
    dist = [1]
    visited[1, 1] = true
    directions = [CartesianIndex(i, j) for i in -1:1, j in -1:1 if i != 0 || j != 0]
    res = 0
    while !visited[end, end]
        frt = popfirst!(q)
        dst = popfirst!(dist)
        for dir in directions
            next_coord = frt + dir
            next_coord ∉ CartesianIndices(mat) && continue
            visited[next_coord] && continue
            visited[next_coord] = true
            if mat[next_coord] == 0
                push!(q, next_coord)
                push!(dist, dst + 1)
                res = dst + 1
            end
        end
    end
    return res
end

# @lc code=end

shortest_path_binary_matrix (generic function with 1 method)

This page was generated using DemoCards.jl and Literate.jl.